Applications

Les calculs pratiques de perte de charge dans les conduites

Expérience de Nikuradsé

L'expérience de Nikuradsé a pour but de déterminer l'influence de la rugosité des parois sur le coefficient de perte de charge linéaire. Les parois d'une conduite sont rendues artificiellement rugueuses en y collant des grains de sable calibrés. En changeant la taille des grains on change la rugosité et on trace \(log \lambda\) en fonction de \(log R\). On appelle ks la taille moyenne des grains collés et \(D\) le diamètre de la conduite. \(ks / D\) est la rugosité relative. On remarque :

1- la rugosité n'a pas d'influence en régime laminaire et le nombre de Reynolds critique \(Rc\) est indépendant de la rugosité.

2- quand \(R > Rc\) la perte de charge dépend fortement de \(ks /D\) ou du nombre de reynolds.

3- quand \(R >>> Rc\) la perte de charge ne dépend pas du nombre de Reynolds, elle ne dépend que de \(ks / D\).

Le coefficient de perte de charge est donné par :

Régime laminaire (R < 2000) \(\lambda = \frac{64}{R}\)

Régime turbulent lisse (R > 2000 et ks / D < 1 / 30) \(\lambda = 0.316 R ^{-1/4}\)

Régime turbulent rugueux ( R >>> 2000) \(\lambda = 0.79 \sqrt{\frac{k_S}{D}}\)

Il existe d'autres expressions des coefficients de pertes de charge en fonction des modèles utilisés par les auteurs. Par exemple pour les écoulements turbulents, on peut utiliser la formule de Colebrook et White :

\[\frac{1}{\sqrt{\lambda}} = -2 log [\frac{2.51}{R \sqrt{\lambda}} + \frac{k_S}{3.71 D}]\]

Diagramme de Moody

Explications

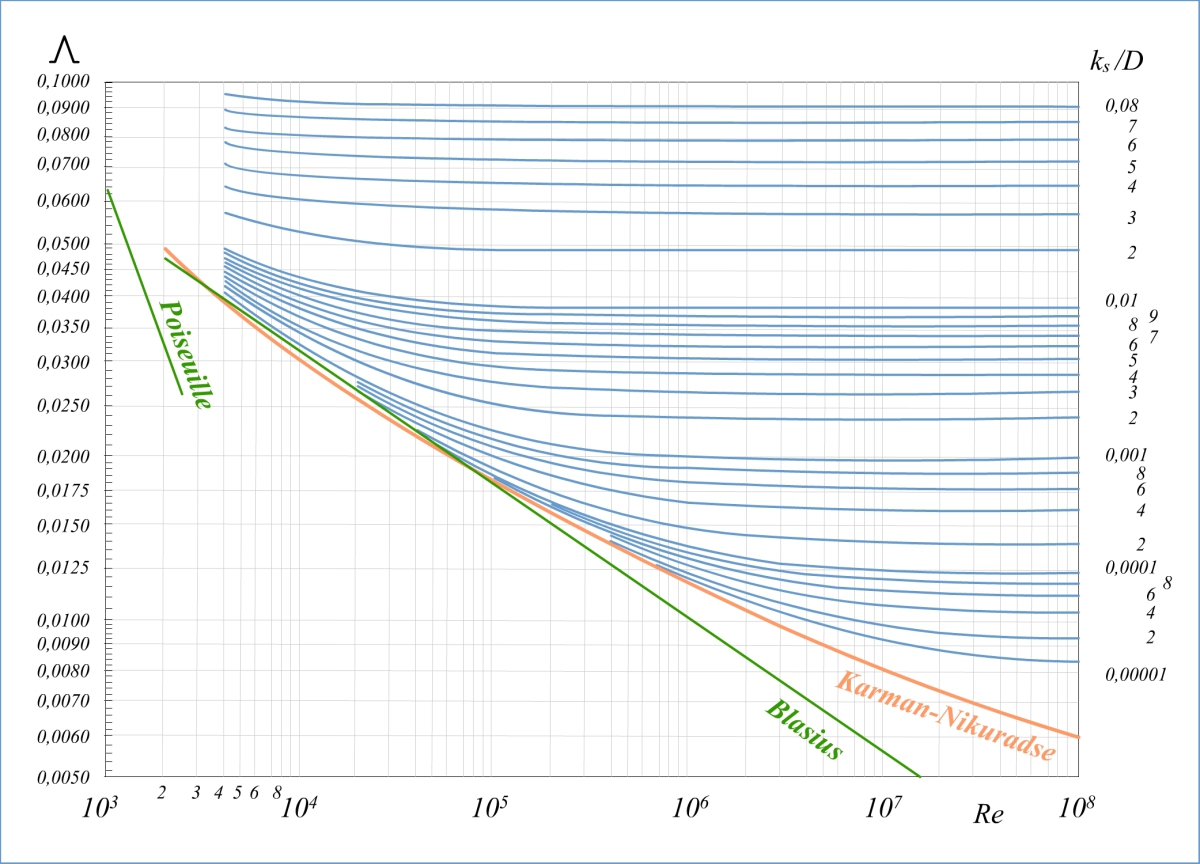
En pratique, on utilise des abaques appelées diagramme de Moody qui représentent le coefficient de perte de charge en fonction du nombre de Reynolds et de la rugosité relative (cliquez sur l'image pour zoomer) :

Puissance dissipée

Explications

On considère une conduite cylindrique de diamètre D, de longueur L, le fluide a une vitesse moyenne w en écoulement suivant z. On a :

\[R = \frac{D \overline{w}}{v} = \frac{\rho D \overline{w}}{ \mu}\]

La perte de charge s'écrit :

\[\Delta H = \lambda \frac{L}{D} \frac{\overline{w}^2}{2 g} \mbox{ en mètre}\]

\(\lambda\) est trouvé par les méthodes précédentes.

La puissance dissipée (en watt) s'écrit :

\[P = \rho g q_v \Delta H\]