Applications
Méthode de Raleigh
Pertes de charge dans une conduite
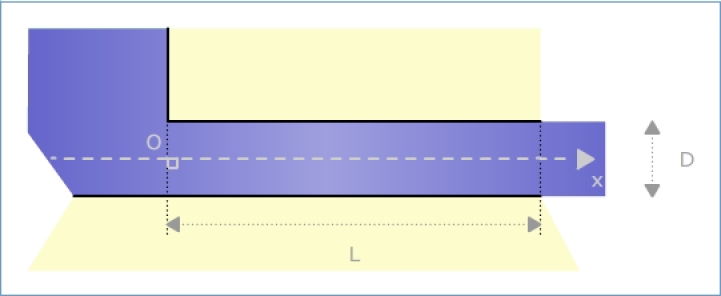
Données : V : vitesse moyenne de l'écoulement, H1 charge en x=0, H2 charge en x=L, ks diamètre moyen des aspérités des parois, D diamètre de la conduite, ρ masse volumique et μ viscosité dynamique.
But : déterminer la perte de charge linéaire : j = (P1 – P2) / L
Méthode
a- inventaire de tous les paramètres en fonction des unités fondamentales : m, kg, s, K
b- Recherche de l'expression de j
(k sans dimension)
Nous avons 5 paramètres et 3 unités fondamentales (kg, m,s); l'analyse dimensionnelle donne :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Par identification, on obtient :
Afin, d'exprimer les grandeurs réduites, on écrit 3 inconnues en fonction des deux autres, soit :
Expression de la perte de charge linéaire
On peut donc exprimer la perte de charge linéaire sous la forme :
Pour mettre en évidence les grandeurs réduites et les conditions de similitude, écrivons l'expression précédente sous la forme :
Conditions de similitude
Dans l'expression précédente, on reconnaît :
Le coefficient de perte de charge s'écrit :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Dans une étude sur maquette et sur prototype, les conditions de similitude sont donc les suivantes :
La méthode de Rayleigh ne fournit que la forme de la loi du phénomène étudié, seule l'expérience dit si cette loi existe.
Attention : Difficulté
Il ne faut oublier aucun paramètre intervenant dans le phénomène étudié
(l 'étude physique doit être minutieuse)
Pour retrouver ce résultat, il est conseillé de faire l'Exercice 2.