Applications
Remarques
Une équation dynamique est insuffisante pour une étude complète d'un écoulement.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Les caractéristiques de l'écoulement d'un fluide sont données par :
- la vitesse : \(V\)
- la pression : \(P\)
- la masse volumique :\(\rho\)
- la température : \(T\)
L'équation d'Euler doit donc être complétée par d'autres équations caractérisant le fluide, son mouvement et les conditions d'écoulement.
Eléments à ajouter
Il faut donc ajouter :
- l'équation de conservation de la masse : \(\mbox{div} (\rho \overrightarrow{V}) + \frac{\partial \rho}{\partial t} = \rho Q\) avec Q le débit volumique de production
- l'équation d'état du fluide :\(f (P, \rho, T) = 0\)
- l'équation caractérisant le type de transformation subie par le fluide (incompressible, isotherme, adiabatique...).
- les conditions aux limites et les conditions initiales qui permettent de déterminer les constantes d'intégration.
Exemple : Équation caractéristique du fluide
\(f(P, \rho, T)=0\)
- liquide incompressible : \(\rho = f(T)\)
- liquide légèrement compressible : \(\rho = \rho_0(T) (1 + k P)\)
- Gaz parfait : \(\frac{P}{\rho} = r T\)
Attention : Transformations subies
Dans le cas de transformations réversibles :
Pour les isothermes : \(\rho = cste\) (fluide incompressible) et \(\frac{P}{\rho} =cste\) (gaz parfait).
Pour les transformations adiabatiques : \(\rho = cste\) (fluide incompressible) et \(\frac{P}{\rho ^y} =cste\) (gaz parfait).
Exemple : Conditions aux limites
Elles sont définies par des parois fixes ou mobiles ou par des surfaces libres.
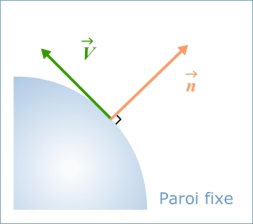
Paroi fixe
L'équation de la paroi est donnée par : F(x, y, z) = 0
En fluide parfait la vitesse est nécessairement orthogonale à la paroi; cette normale est définie par le gradient de la fonction F(x,y,z); la condition aux limites s'écrit donc :
vi est la projection de la vitesse sur x, y ou z et le deuxième terme représente les coordonnées du gradient de F.
Paroi mobile
On ajoute simplement à l'équation précédente le terme dépendant du temps, soit :
Surface libre
\(P = constante\)